WAMS - Winternitz Abstract Merkle Signature Scheme


  Author: Herman Schoenfeld 
  Version: 1.1
  Date: 2020-07-20
  Copyright: (c) Sphere 10 Software Pty Ltd. All Rights Reserved.
WAMS.pdf

Original e-print

Abstract

A quantum-resistant, many-time signature scheme combining Winternitz and Merkle-Signature schemes is proposed. This construction is compatible with the Abstract Merkle Signature (AMS) Scheme [1] and thus is an AMS-algorithm called "WAMS".

1. Introduction

WAMS is a specialization of the AMS [1] scheme parameterized with the standard Winternitz one-time signature scheme (W-OTS). WAMS is a quantum-resistant cryptographic scheme suitable for blockchain-based applications.

This document focuses only on the OTS-layer of WAMS. The merkle signatures themselves are performed as part of the AMS-layer of WAMS which is defined in the AMS document [1] . The reader should familiarize themselves with the AMS document as it provides the background context for AMS-algorithms of which WAMS is one.

2. WAMS Scheme

The Winternitz Abstracted Merkle Signature (WAMS) Scheme is a general purpose, quantum-resistant digital signature scheme. WAMS is an AMS algorithm that selects the standard Winternitz OTS (W-OTS) as the OTS parameter. As part of the parameter set inherited from AMS, WAMS includes the additional parameters H, a cryptographic hash function and w, the Winternitz parameter.

The selected cryptographic hash function H is fundamental to the security of WAMS, an analysis of which is not provided in this document. So long as the user selects a standard Cryptographic Hash Function (CHF) such as SHA2-256 or Blake2b the security of WAMS is equivalent to standard W-OTS constructions. For performance, the use of W-OTS# [4] may be used in conjunction with Blake2b-128 in order to reduce signature sizes without introducing vulnerability to birthday-class attacks.

In the presented construction herein, the Winternitz parameter w refers to the number of bits being simultaneously signed as famously proposed by Merkle [3] (who was inspired by Winternitz). Varying the parameter w changes the size/speed trade-off without affecting security. For example, the higher the value the more expensive (and slower) the computations but the shorter the signature and private key size. The lower the value the faster the computation but larger the signature and key size. The range of values for w supported in WAMS is 1 <= w <= 16.

Since the WAMS scheme inherits the AMS scheme, it is required to define the following:

  • The OTS private key which is a standard W-OTS private key.
  • The OTS public key is a standard W-OTS public key (hash).
  • Definitions for GenOTSSig and VerOTSSig which generate and verify W-OTS signatures in accordance to the WAMS1specification.

Definitions for all of the above are provided below.

2.1 Notation & Definitions

  1. Notations and definitions from AMS [1] are inherited by this document.
  2. ReadBits(arr, N, M) is a function that skips N bits and then reads M bits from the byte array arr and re-interprets the bits as a big-endian unsigned 32-bit integer.
  3. WriteBits(x, arr, N, M) is a function that converts unsigned 32-bit integer x to big-endian byte array of 4 bytes and writes the first M bits of the array into array arr start at bit offset N.
  4. Bit-ordering in (2) and (3) is such that bit i of arr maps to byte arr[i SHR 3] and to in-byte bit-index (i SHR 3) - (i SHL 3). Explained below: 

Bit-ordering within `ReadBits` and `WriteBits` are such that the
   least-significant bit (LSB) is the left-most bit of that byte.

   For example, consider an array of two bytes C = [A,B]:

   Memory layout of C=[a,b] with their in-byte indexes marked.
   A:[7][6][5][4][3][2][1][0]  B:[7][6][5][4][3][2][1][0]
   C:[0][1][2][3][4][5][6][7]    [8][9]...

   The bit indexes of the 16-bit array C are such that:
     Bit 0 maps to A[7]
     Bit 1 maps to A[6]
     Bit 7 maps to A[0]
     Bit 8 maps to B[7]
     Bit 16 maps to B[0]

2.2 WAMS Parameters

Parameters Description Bits
h Tree height (used in AMS layer) 8
w Winternitz parameter, how many bits are simultaneously signed via the Winternitz gadget 8
H Cryptographic hash function, and security parameter for the scheme (digest length) 8

Note that the Winternitz w and H are stored in the RESERVED part of the AMS private key. The cryptographic hash function is stored as a code, defined as follows:

2.2.1 Cryptographic Hash Function Code

Value Cryptographic Hash Function
0 user specified
1 SHA2-256
2 Blake2b-256
3 Blake2b-160
4 Blake2b-128

The author reserves the right to update this list as new use-cases emerge.

2.3 WAMS Variables

During key generation, signing and verification the following variables are calculated based on the parameter set.

Variable Formula Description
U sizeof(H(x)) * 8 for any x Security parameter for the scheme (and number of bits in a hash H)
DigitBase 2^w The number of values a signed "digit" can take
SigDigits ceil(256 / w) Number of digits in the message-digest being signed
CheckDigits Log((2^w - 1) * (256/w))_{2^w} Number of digits in checksum being signed
OTS_KeyDigits SigDigits + CheckDigits Number of "digit keys" in a W-OTS private key (used by AMS-layer)
OTS_SigLen OTS_KeyDigits Number of "digit signatures" in a W-OTS sig (used by AMS-layer)

2.4 W-OTS Theory Basics

The W-OTS scheme follows the Lamport [5] signature approach but allows a signer to sign w bits of a message-digest simultaneously rather than 1. This collection of bits is a treated as a "digit" of base 2^w.

For example, in the case of w=8 the digits simply become bytes since each digit can take any value within 0..255. The fundamental cryptographic mechanism in W-OTS is the ability to sign individual digits using a unique "digit private key".

For example, to sign the byte b (for w=8), a signer first derives a "private digit key" as K = H(secret) and a "public digit key" P = H^255(K). Notice that all the values of b map to a unique hash in that chain of hashes. The signer advertises the "public digit key" prior to signing any digit. When signing a digit b, the signer provides the verifier the value S=H^(255-b)(K) referred to as the "signature of b". The verifier need only perform b more iterations on the signature s to arrive at the public key P, since H^b(S) = H^b(H^(255-b)(K)) = H^255(K) = P.

At this point, the verifier has cryptographically determined the signer had knowledge of K since the signature S was the b'th pre-image of P. This process of signing digits is repeated for each digit in the message and each digit signature is concatenated to form the signature. The message being signed is always a digest of an actual logical message, and thus referred to as the "message-digest".

In W-OTS, the individual "digit keys" and "digit signatures" are concatenated to comprise the "key" and "signatures" respectively. This results in order of magnitude larger key and signature objects when compared to traditional elliptic-curve / discrete logarithm schemes. This is a significant down-side of OTS schemes when used in post-quantum cryptography (PQC) use cases. The burden of large keys can be optimized by using the hash of a public key as WAMSD prescribes. The burden of large signatures can be halved by choosing shorter hash functions without impacting security, as prescribed by the W-OTS# [4] variant.

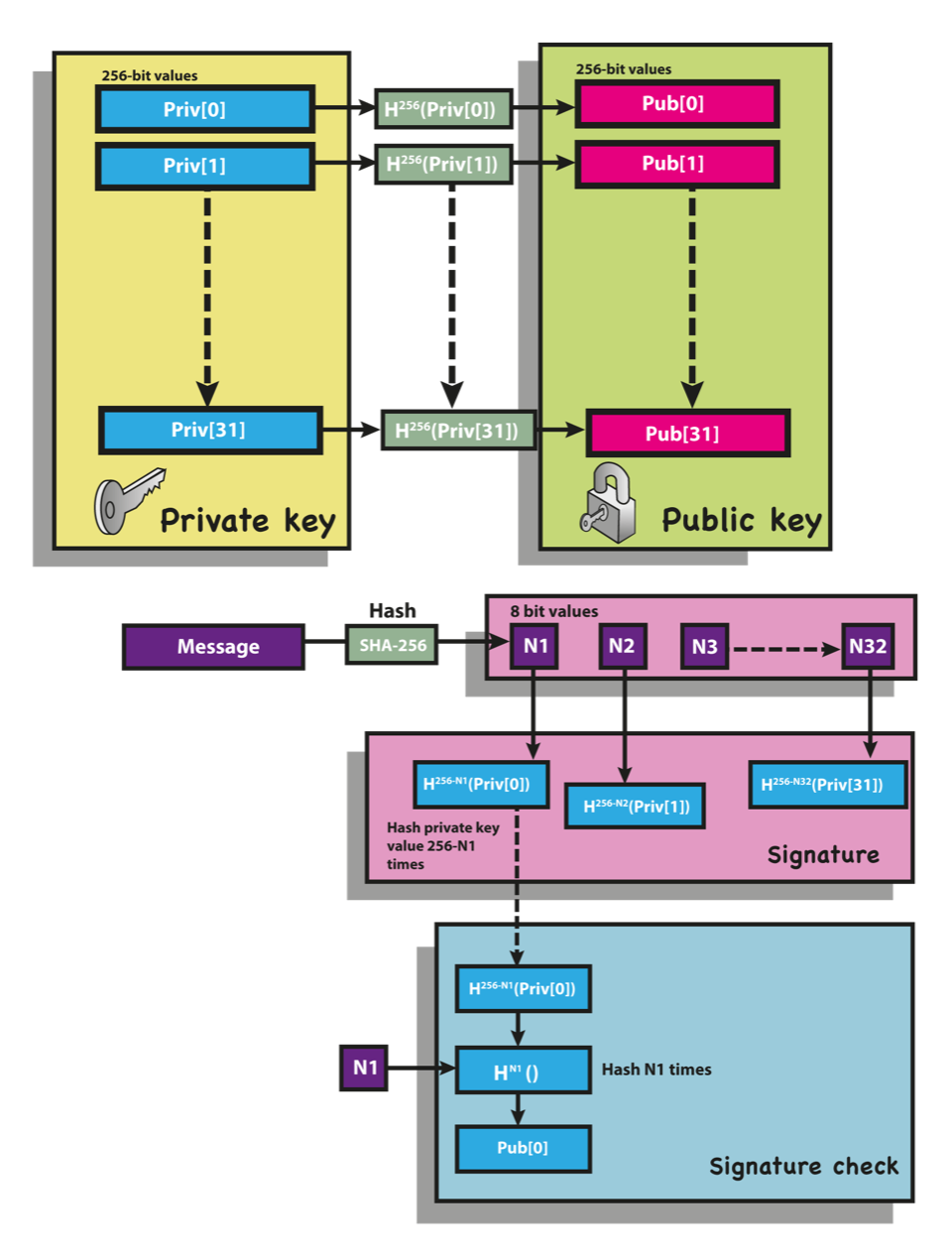
Diagram 1: Winternitz One-Time Signature gadget (courtesy Sphere 10 Software<a class= [2] )">
Diagram 1: Winternitz One-Time Signature gadget (courtesy Sphere 10 Software [2] )
NOTE In order to prevent signature forgeries arising from digit signature re-use for prior messages, a checksum is calculated and appended to the message-digest and signed alongside the digest. The checksum is calculated in such a way that any increment to a message digit necessarily decreases a checksum digit. Thus it is impossible to forge a signature since it requires the pre-image of at least one checksum digit signature.

The reader can further their understanding of the theory and basics of W-OTS by reviewing the literature and through the below succinct Diagram 1 .

2.4.1 W-OTS Private Key

A W-OTS private key P' is a one-time key used to generate W-OTS signatures and defined as follows: 


1: P' = byte-array[OTS_KeyDigits, U/8]
2: for n in {0, OTS_KeyDigits - 1}
3:    P'[n] = cryptographically random U bits

The W-OTS private key is an array of OTS_KeyDigits "digit keys" each of U/8 bytes in length. The total size of the W-OTS private key is thus (OTS_KeyDigits) * (U/8) bytes.

Whilst the W-OTS scheme requires that private keys be cryptographically random, they can be deterministically derived from a secret seed. In WAMS the AMS Private Key is used (see below).

2.4.2 W-OTS Public Key Hash

A W-OTS public key hash K' is a one-time key used to verify W-OTS signatures signed by a W-OTS private key P' and defined as follows: 


1: k = byte-array[OTS_KeyDigits, U/8]
2: for n in {0, OTS_KeyDigits - 1}
3:    k[n] = H^(DigitBase - 1)( P'[n] )
4: K' = H( k[0] || k[1] || ... || k[OTS_KeyDigits - 1] )

The length of a W-OTS public key hash is U/8 bytes.

NOTE In WAMS, the W-OTS public key hash is used rather than the W-OTS public key since signature verification always rebuilds the public key from the signature. Since the verifier derives the public key it can derive the public key hash with one additional step. By using the hash rather than the key in the AMS signature, a ~50% space saving is made to the AMS signature length.
NOTE Since the OTS layer passes the public key hash to the AMS layer, the AMS layer does not need hash the public keys when building the hash-tree of OTS keys, it simply re-uses the OTS public key value which is itself a hash digest (saving 2^h hash computations when computing a batch).

2.5 WAMS Key Generation

Given a AMS Private Key P and batch number B, the i'th W-OTS key-pair ( P', K') are derived as follows: 


 1: algorithm GenOTSKeys
 2:   Input:
 3:         P: AMS Private Key
 4:         B: batch number (UInt64)
 5:         i: index (UInt16)
 6:   Output:
 7:         P': the W-OTS private key that derives K'
 8:         K': the i'th W-OTS public key hash in the batch
 9:   Pseudo-Code:
10:     P' = byte-array[OTS_KeyDigits, U/8]
11:     k = byte-array[OTS_KeyDigits, U/8]
12:     let seed = ToBytes(i) || ToBytes(B) || P
13:     for n in {0, OTS_KeyDigits - 1}
14:        P'[n] = H^2( n || seed )
15:        k[n] = H^(DigitBase - 1) ( P'[n] )
16:     K' = H( k[0] || k[1] || ... || k[OTS_KeyDigits - 1] )
17: end algorithm

2.6 W-OTS Signature Generation

A W-OTS signature is an 2D array of bytes of dimensions [OTS_KeyDigits, U/8] and generated as follows: 


 1: algorithm GenOTSSig
 2:   Input:
 3:         m: a message-digest (U/8 bytes)
 4:         P': a W-OTS private key
 5:   Output:
 6:         S': a W-OTS signature
 7:   Pseudo-Code:
 8:     S' = byte-array[OTS_KeyDigits, U/8]
 9:     // sign message part
10:     let c = 0                     ; checksum value
11:     for n in {0, SigDigits - 1}
12:        let v = 2^w - ReadBits(m, w*n, w) - 1
13:        c = c + v;
14:        S'[n] = H^v( P'[n] )
15:
16:     // sign checksum part
17:     let c_bytes = byte-array[4]
19:     WriteBits(c, c_bytes, 0, 32)
20:     for n in {0, CheckDigits - 1}
21:        let v = 2^w - ReadBits(c_bytes, w*n, w) - 1
22:        S'[SigDigits + n] = H^v( P'[SigDigits + n] )
24: end algorithm

2.7 W-OTS Signature Verification

Here a W-OTS signature is verified to a W-OTS public key hash by rebuilding the W-OTS public key from the signature, hashing it and comparing with public key hash provided by the AMS layer. 


  1: algorithm VerOTSSig
  2:   Input:
  3:        S': a W-OTS signature (byte[ OTS_KeyDigits, U/8 ])
  4:        m: a message-digest (byte[U/8])
  5:        K': W-OTS public key/hash (byte[U/8])
  6:   Output: Boolean
  7:   Pseudo-Code:
  8:        k = byte[ OTS_KeyDigits, U/8 ]    ; the W-OTS public key
  9:        ; verify message part
 10:        let c = 0                         ; checksum value
 11:        for n in {0, SigLen - 1}
 12:           let d = ReadBits(m, w * n, w)  ; note: d + v = 2^w - 1
 13:           c = 2^w + d - 1
 14:           k[n] = H^d( S'[n] )            ; note: k[n] = H^d(H^c(P'[n]))
 15:
 16:        ; verify checksum part
 17:        let c_bytes = byte-array[4]
 18:        WriteBits(c, c_bytes, 0, 32)
 19:        for n in {0, CheckDigits - 1}
 20:           let d = ReadBits(c_bytes, w * n, w)
 21:           k[SigDigits + n] = H^d( S'[SigDigits + n] )
 22:
 23:        ; compare pub key hash
 24:        let PKH = H( k[0] || k[1] || ... || k[OTS_KeyDigits - 1] )
 25:        return (K' = PKH)                ; check sig rebuilt the public key hash
 26: end algorithm

3. WAMS#

WAMS# is a variant of WAMS which selects W-OTS# [4] rather than W-OTS as the OTS. W-OTS# is virtually identical to W-OTS except the message-digest is salted to harden the signature security to a sufficient level that thwarts birthday-class attacks. This allows the selection of shorter hash functions which produce shorter and faster signatures for same security as W-OTS.

The WAMS# implementation is virtually identical to WAMS except for the following changes:

  1. A cryptographically random salt R of Ubits is generated during signing.
  2. For any message m, the signer signs the "sig-mac" SMAC(m, R) rather than the message-digest H(m) which is defined as
    SMAC(m, R) = H(R || H (R || H(m))) .
  3. R is appended to the signature.
  4. During verification, the verifier similarly verifies SMAC(m, R) rather than the ordinary message-digest.

The reader is referred to the reference implementation of WAMS# which succinctly overloads WAMS with these minor changes.

4. Object Lengths & Throughput

A C# implementation in .NET 7 was developed and object lengths and performance metrics are measured below. All tests were performed on a single thread on an Intel Core i9-10900K CPU 3.70 GHz with 32GB RAM. The implementation was not performance tuned so the throughput metrics are useful when compared relative to each other.

OTS CHF bits Winternitz w Height h Public Key Length (b) Signature Length (b) Sign Throughput Verify Throughput
W-OTS 128 2 0 32 2163 3620 18098
W-OTS# 128 2 0 32 2211 3425 13139
W-OTS 128 2 8 32 2163 3832 17919
W-OTS# 128 2 8 32 2211 3523 12056
W-OTS 128 2 16 32 2163 3759 18137
W-OTS# 128 2 16 32 2211 3528 12111
W-OTS 128 4 0 32 1107 2821 11479
W-OTS# 128 4 0 32 1155 2619 10403
W-OTS 128 4 8 32 1107 2803 13454
W-OTS# 128 4 8 32 1155 2610 9861
W-OTS 128 4 16 32 1107 2810 13470
W-OTS# 128 4 16 32 1155 2602 9515
W-OTS 128 8 0 32 579 432 2406
W-OTS# 128 8 0 32 627 414 2079
W-OTS 128 8 8 32 579 434 2403
W-OTS# 128 8 8 32 627 419 2749
W-OTS 128 8 16 32 579 432 2411
W-OTS# 128 8 16 32 627 404 2749
W-OTS 160 2 0 36 2703 3850 17026
W-OTS# 160 2 0 36 2763 3607 11620
W-OTS 160 2 8 36 2703 3828 16875
W-OTS# 160 2 8 36 2763 3567 11800
W-OTS 160 2 16 36 2703 3871 16969
W-OTS# 160 2 16 36 2763 3551 11572
W-OTS 160 4 0 36 1383 2864 12419
W-OTS# 160 4 0 36 1443 2702 9318
W-OTS 160 4 8 36 1383 2841 12564
W-OTS# 160 4 8 36 1443 2685 9841
W-OTS 160 4 16 36 1383 2854 12586
W-OTS# 160 4 16 36 1443 2680 9120
W-OTS 160 8 0 36 723 434 2154
W-OTS# 160 8 0 36 783 417 2184
W-OTS 160 8 8 36 723 428 2145
W-OTS# 160 8 8 36 783 422 2425
W-OTS 160 8 16 36 723 427 2156
W-OTS# 160 8 16 36 783 421 2032
W-OTS 256 2 0 48 4323 3937 12474
W-OTS# 256 2 0 48 4419 3662 9235
W-OTS 256 2 8 48 4323 3951 12275
W-OTS# 256 2 8 48 4419 3620 8829
W-OTS 256 2 16 48 4323 3905 12373
W-OTS# 256 2 16 48 4419 3666 9168
W-OTS 256 4 0 48 2211 3059 8653
W-OTS# 256 4 0 48 2307 2885 7711
W-OTS 256 4 8 48 2211 3081 8549
W-OTS# 256 4 8 48 2307 2873 7151
W-OTS 256 4 16 48 2211 3025 8527
W-OTS# 256 4 16 48 2307 2865 7035
W-OTS 256 8 0 48 1155 485 1299
W-OTS# 256 8 0 48 1251 464 1849
W-OTS 256 8 8 48 1155 489 1345
W-OTS# 256 8 8 48 1251 471 1372
W-OTS 256 8 16 48 1155 487 1331
W-OTS# 256 8 16 48 1251 458 1502

Throughput is measured in "Signatures Per Second"

5. Reference Implementation

This section contains snippets for the full reference implementation [6] . The reference implementation is part of the PQC library within the Hydrogen Framework [7] .

5.1 AMS-Compatible W-OTS

This implementation of W-OTS can be used as an OTS within the AMS implementation [1] . 


public class WOTS : IOTSAlgorithm {

	public WOTS() 
		: this(Configuration.Default) {
	}

	public WOTS(int w, bool usePublicKeyHashOptimization = false)
		: this(w, Configuration.Default.HashFunction, usePublicKeyHashOptimization) {
	}

	public WOTS(int w, CHF hashFunction, bool usePublicKeyHashOptimization = false)
		: this(new Configuration(w, hashFunction, usePublicKeyHashOptimization)) {
	}

	public WOTS(Configuration config) {
		Config = (Configuration)config.Clone();
	}

	public Configuration Config { get; }

	OTSConfig IOTSAlgorithm.Config => Config;

	public void SerializeParameters(Span buffer) {
		buffer[0] = (byte)Config.W;
	}

	public byte[,] GeneratePrivateKey() 
		=> GenerateKeys().PrivateKey;

	public byte[,] DerivePublicKey(byte[,] privateKey) {
		var publicKey = new byte[Config.KeySize.Length, Config.KeySize.Width];
		for (var i = 0; i < Config.KeySize.Length; i++) {
			publicKey.SetRow(i,  Hashers.Iterate(Config.HashFunction, privateKey.GetRow(i), Config.ChainLength));
		}
		return Config.UsePublicKeyHashOptimization ? ToOptimizedPublicKey(publicKey): publicKey;
	}

	public OTSKeyPair GenerateKeys() 
		=> GenerateKeys(Tools.Crypto.GenerateCryptographicallyRandomBytes(Config.DigestSize - 1));

	public OTSKeyPair GenerateKeys(ReadOnlySpan seed) {
		var enumeratedSeed = new byte[seed.Length + 1];
		seed.CopyTo(enumeratedSeed.AsSpan(1));
		return GenerateKeys(i => {
			enumeratedSeed[0] = (byte)i;
			return Hashers.Iterate(Config.HashFunction, enumeratedSeed, 2);
		});
	}

	public OTSKeyPair GenerateKeys(Func gen) {
		var priv = new byte[Config.KeySize.Length, Config.KeySize.Width];
		var pub = new byte[Config.KeySize.Length, Config.KeySize.Width];  // actual W-OTS pubkey is same size as priv key, we may optimize below
		for (var i = 0; i < Config.KeySize.Length; i++) {
			var randomBytes = gen(i);
			priv.SetRow(i, randomBytes);
			pub.SetRow(i, Hashers.Iterate(Config.HashFunction, randomBytes, Config.ChainLength));
		}

		IFuture pubKeyHash;
		if (Config.UsePublicKeyHashOptimization) {
			pub = ToOptimizedPublicKey(pub);
			pubKeyHash = ExplicitFuture.For(pub.ToFlatArray());
		} else {
			pubKeyHash = LazyLoad.From(() => ToOptimizedPublicKey(pub).ToFlatArray());
		}

		return new OTSKeyPair(priv, pub, pubKeyHash);
	}

	[MethodImpl(MethodImplOptions.AggressiveInlining)]
	public virtual byte[,] Sign(byte[,] privateKey, ReadOnlySpan message) 
        => SignDigest(privateKey, ComputeMessageDigest(message));

	[MethodImpl(MethodImplOptions.AggressiveInlining)]
	public virtual byte[,] SignDigest(byte[,] privateKey, ReadOnlySpan digest) {
		var signature = new byte[Config.SignatureSize.Length, Config.SignatureSize.Width];

		// Sign the digest (and build the checksum in process)
		uint checksum = 0U;
		for (var i = 0; i < Config.SignatureDigits; i++) {
			var signValue = (int)Bits.ReadBinaryNumber(digest, Config.W * i, Config.W, IterateDirection.LeftToRight);
			var c = Config.ChainLength - signValue;
			checksum += (uint)c;
			signature.SetRow(i, Hashers.Iterate(Config.HashFunction, privateKey.GetRow(i), c));
		}

		// Sign the checksum
		var checksumBytes = new byte[4];
		Bits.WriteBinaryNumber(checksum, checksumBytes, 0, 32, IterateDirection.LeftToRight);
		for (var i = 0; i < Config.ChecksumDigits; i++) {
			var signValue = (int)Bits.ReadBinaryNumber(checksumBytes, Config.W * i, Config.W, IterateDirection.LeftToRight);
			var c = Config.ChainLength - signValue;
			var row = Config.SignatureDigits + i;
			signature.SetRow(row, Hashers.Iterate(Config.HashFunction, privateKey.GetRow(row), c));
		}

		return signature;
	}

	[MethodImpl(MethodImplOptions.AggressiveInlining)]
	public bool Verify(byte[,] signature, byte[,] publicKey, ReadOnlySpan message) 
        =>  VerifyDigest(signature, publicKey, ComputeMessageDigest(message));

	public virtual bool VerifyDigest(byte[,] signature, byte[,] publicKey, ReadOnlySpan digest) {
		var verify = new byte[Config.KeySize.Length, Config.KeySize.Width];

		// Verify Digest
		uint checksum = 0U;
		for (var i = 0; i < Config.SignatureDigits; i++) {
			var signValue = (int)Bits.ReadBinaryNumber(digest, Config.W * i, Config.W, IterateDirection.LeftToRight);
			var c = Config.ChainLength - signValue;
			checksum += (uint)c;
			verify.SetRow(i, Hashers.Iterate(Config.HashFunction, signature.GetRow(i), signValue));
		}

		// Verify checksum
		var checksumBytes = new byte[4];
		Bits.WriteBinaryNumber(checksum, checksumBytes, 0, 32, IterateDirection.LeftToRight);
		for (var i = 0; i < Config.ChecksumDigits; i++) {
			var signValue = (int)Bits.ReadBinaryNumber(checksumBytes, Config.W * i, Config.W, IterateDirection.LeftToRight);
			var row = Config.SignatureDigits + i;
			verify.SetRow(row, Hashers.Iterate(Config.HashFunction, signature.GetRow(row), signValue));
		}

		return (Config.UsePublicKeyHashOptimization ? this.ComputeKeyHash(verify): verify.AsFlatSpan()).SequenceEqual(publicKey.AsFlatSpan());
	}

	[MethodImpl(MethodImplOptions.AggressiveInlining)]
	public void ComputeKeyHash(byte[,] key, Span result) {
		ComputeKeyHash(key.AsFlatSpan(), result);
	}

	[MethodImpl(MethodImplOptions.AggressiveInlining)]
	public void ComputeKeyHash(ReadOnlySpan key, Span result) {
		Hashers.Hash(Config.HashFunction, key, result);
	}

	[MethodImpl(MethodImplOptions.AggressiveInlining)]
	protected byte[,] ToOptimizedPublicKey(byte[,] publicKey) {
		var publicKeyHash = new byte[1, Config.DigestSize];
		ComputeKeyHash(publicKey, publicKeyHash.AsFlatSpan());
		return publicKeyHash;
	}

	[MethodImpl(MethodImplOptions.AggressiveInlining)]
	public byte[] ComputeMessageDigest(ReadOnlySpan message)
		=> Hashers.Hash(Config.HashFunction, message);

	
	public class Configuration : OTSConfig {
		public static readonly Configuration Default;

		static Configuration() {
			Default = new Configuration(8, CHF.SHA2_256, false);
		}

		public Configuration(): this(Default.W, Default.HashFunction, Default.UsePublicKeyHashOptimization) {
		}

		public Configuration(int w, CHF hasher, bool usePubKeyHashOptimization) 
			: this(
				  w,
				  hasher,
				  usePubKeyHashOptimization,
				  AMSOTS.WOTS, 
				  Hashers.GetDigestSizeBytes(hasher), 
				  new OTSKeySize(
					  Hashers.GetDigestSizeBytes(hasher), 
					  (int)Math.Ceiling(256.0 / w) + (int)Math.Floor(Math.Log(((1 << w) - 1) * (256 / w), 1 << w)) + 1
				  ),
  				new OTSKeySize(
					Hashers.GetDigestSizeBytes(hasher),
					usePubKeyHashOptimization ? 1 : (int)Math.Ceiling(256.0 / w) + (int)Math.Floor(Math.Log(((1 << w) - 1) * (256 / w), 1 << w)) + 1
				),
				new OTSKeySize(
			        Hashers.GetDigestSizeBytes(hasher),
					(int)Math.Ceiling(256.0 / w) + (int)Math.Floor(Math.Log(((1 << w) - 1) * (256 / w), 1 << w)) + 1
				)
			) {
		}

		protected Configuration(int w, CHF hasher, bool usePubKeyHashOptimization, AMSOTS id, int digestSize, OTSKeySize keySize, OTSKeySize publicKeySize, OTSKeySize signatureSize) 
			: base(id, hasher, digestSize, usePubKeyHashOptimization, keySize, publicKeySize, signatureSize) {
			Guard.ArgumentInRange(w, 1, 16, nameof(w));
			W = (byte)w;
			ChainLength = (1 << w) - 1; // 2^w - 1 (length of Winternitz chain)
			SignatureDigits = (int)Math.Ceiling(256.0 / w); // how many chains required; 
			ChecksumDigits = (int)Math.Floor(Math.Log(((1 << w) - 1) * (256 / w), 1 << w)) + 1; // floor ( log_b (2^w - 1) * (256/w) ) where b = 2^w
		}

		public int W { get; }

		public int ChainLength { get; }

		public int SignatureDigits { get; }

		public int ChecksumDigits { get; }

		public override object Clone() => new Configuration(W, HashFunction, UsePublicKeyHashOptimization, AMSID, DigestSize, KeySize, PublicKeySize, SignatureSize);

	}

}

5.2 AMS-Compatible W-OTS#

This implementation of W-OTS# can be used as an OTS within the AMS implementation [1] . 


public class WOTSSharp : WOTS {

	public WOTSSharp() 
		: this(WOTSSharp.Configuration.Default) {
	}

	public WOTSSharp(int w, bool usePublicKeyHashOptimization = false)
		: this(w, Configuration.Default.HashFunction, usePublicKeyHashOptimization) {
	}

	public WOTSSharp(int w, CHF hashFunction, bool usePublicKeyHashOptimization = false)
		: this(new Configuration(w, hashFunction, usePublicKeyHashOptimization)) {
	}

	public WOTSSharp(Configuration config) 
		: base(config) {
	}

	public override byte[,] SignDigest(byte[,] privateKey, ReadOnlySpan digest)
		=> SignDigest(privateKey, digest, Tools.Crypto.GenerateCryptographicallyRandomBytes(digest.Length));

	public byte[,] SignDigest(byte[,] privateKey, ReadOnlySpan digest, ReadOnlySpan seed) {
		Guard.Argument(seed.Length == digest.Length, nameof(seed), "Must be same size as digest");
		var wotsSig = base.SignDigest(privateKey, HMAC(digest, seed));
		Debug.Assert(wotsSig.Length == Config.SignatureSize.Length * Config.SignatureSize.Width);
		seed.CopyTo(wotsSig.GetRow(Config.SignatureSize.Length - 1)); // concat seed to sig
		return wotsSig;
	}

	public override bool VerifyDigest(byte[,] signature, byte[,] publicKey, ReadOnlySpan digest) {
		Debug.Assert(signature.Length == Config.SignatureSize.Length * Config.SignatureSize.Width);
		var seed = signature.GetRow(Config.SignatureSize.Length - 1);
		return base.VerifyDigest(signature, publicKey, HMAC(digest, seed));
	}

	[MethodImpl(MethodImplOptions.AggressiveInlining)]
	private byte[] SMAC(ReadOnlySpan message, ReadOnlySpan seed)
		=> HMAC(ComputeMessageDigest(message), seed);

	private byte[] HMAC(ReadOnlySpan digest, ReadOnlySpan seed) {
		using (Hashers.BorrowHasher(Config.HashFunction, out var hasher)) {
			hasher.Transform(seed);
			hasher.Transform(digest);
			var innerHash = hasher.GetResult();
			hasher.Transform(seed);
			hasher.Transform(innerHash);
			return hasher.GetResult();
		}
	}

	public new class Configuration : WOTS.Configuration {
		public new static readonly Configuration Default;

		static Configuration() {
			Default = new Configuration(4, CHF.Blake2b_128, true);
		}

		public Configuration(): this(Default.W, Default.HashFunction, Default.UsePublicKeyHashOptimization) {
		}

		public Configuration(int w, CHF hasher, bool usePubKeyHashOptimization)
			: base(
				w,
				hasher,
				usePubKeyHashOptimization,
				AMSOTS.WOTS_Sharp,
				Hashers.GetDigestSizeBytes(hasher),
				new OTSKeySize(
					Hashers.GetDigestSizeBytes(hasher),
					(int)Math.Ceiling(256.0 / w) + (int)Math.Floor(Math.Log(((1 << w) - 1) * (256 / w), 1 << w)) + 1
				),
				new OTSKeySize(
					Hashers.GetDigestSizeBytes(hasher),
					usePubKeyHashOptimization ? 1 : (int)Math.Ceiling(256.0 / w) + (int)Math.Floor(Math.Log(((1 << w) - 1) * (256 / w), 1 << w)) + 1
				),
				new OTSKeySize(
					Hashers.GetDigestSizeBytes(hasher),
					(int)Math.Ceiling(256.0 / w) + (int)Math.Floor(Math.Log(((1 << w) - 1) * (256 / w), 1 << w)) + 1  + 1 // Adds extra row for seed here
				)
			) {
		}
	}
}

6. References

[1]  Herman Schoenfeld. "An Abstract Merkle Signature Scheme (AMS)", 2020. URL: https://vixra.org/abs/2212.0019 .

[2] Sphere 10 Software. "Winternitz One-Time Signature Scheme". URL: https://sphere10.com/articles/cryptography/pqc/wots . Accessed on: 2023-05-09.

[3]  Ralph Merkle. "Secrecy, authentication and public key systems / A certified digital signature". Ph.D. dissertation, Dept. of Electrical Engineering, Stanford University, 1979. URL: http://www.merkle.com/papers/Certified1979.pdf .

[4]  Herman Schoenfeld. "W-OTS# - Shorter and Faster Winternitz Signatures". URL: https://vixra.org/abs/2007.0194 . Accessed on: 2020-07-20.

[5]  L. Lamport. "Constructing digital signatures from a one-way function". Technical Report SRI-CSL-98, SRI International Computer Science Laboratory, Oct. 1979.

[6]: Sphere 10 Software. PQC Library. URL: https://github.com/Sphere10/Hydrogen/tree/master/src/Hydrogen/Crypto/PQC . Accessed 2023-05-09.

[7]: Sphere 10 Software. Hydrogen Framework. URL: https://github.com/Sphere10/Hydrogen . Accessed 2024-05-09