Introduction

The Winternitz One-Time Signature (OTS) scheme is a cryptographic algorithm used for digital signatures that ensures data integrity, authenticity, and non-repudiation. It was introduced by Herbert Winternitz in 1982 as a solution to the key distribution problem in public-key cryptography.

Unlike traditional signature schemes that use a single private key for multiple signatures, Winternitz OTS generates a new private key for each signature, making it highly secure against attacks such as key reuse and forgery. However, care must be taken to not accidently re-use a key for more than one time.

The scheme is based on a one-way function that maps a message to a unique signature, and it is widely used in secure communication protocols, including the Internet of Things (IoT) and blockchain technology. In this introduction, we will discuss the key concepts of the Winternitz OTS scheme, its advantages, and limitations, as well as its applications in modern cryptographic systems.

Winternitz vs Lamport

Winternitz One-Time Signature (OTS) is a variant of the Lamport One-Time Signature (OTS) scheme, which was first introduced by Leslie Lamport in 1979. The Winternitz OTS scheme was proposed by P. Winternitz in 1982 as an improvement over the original Lamport OTS scheme.

The main difference between the two schemes lies in the way the private and public keys are generated. In the original Lamport OTS scheme, the private key is a binary matrix where each row is a randomly generated bit string. The public key is obtained by applying a one-way hash function to each row of the private key matrix. To sign a message, a subset of the rows from the private key matrix is used to generate a signature, and the corresponding rows in the public key matrix are used to verify the signature.

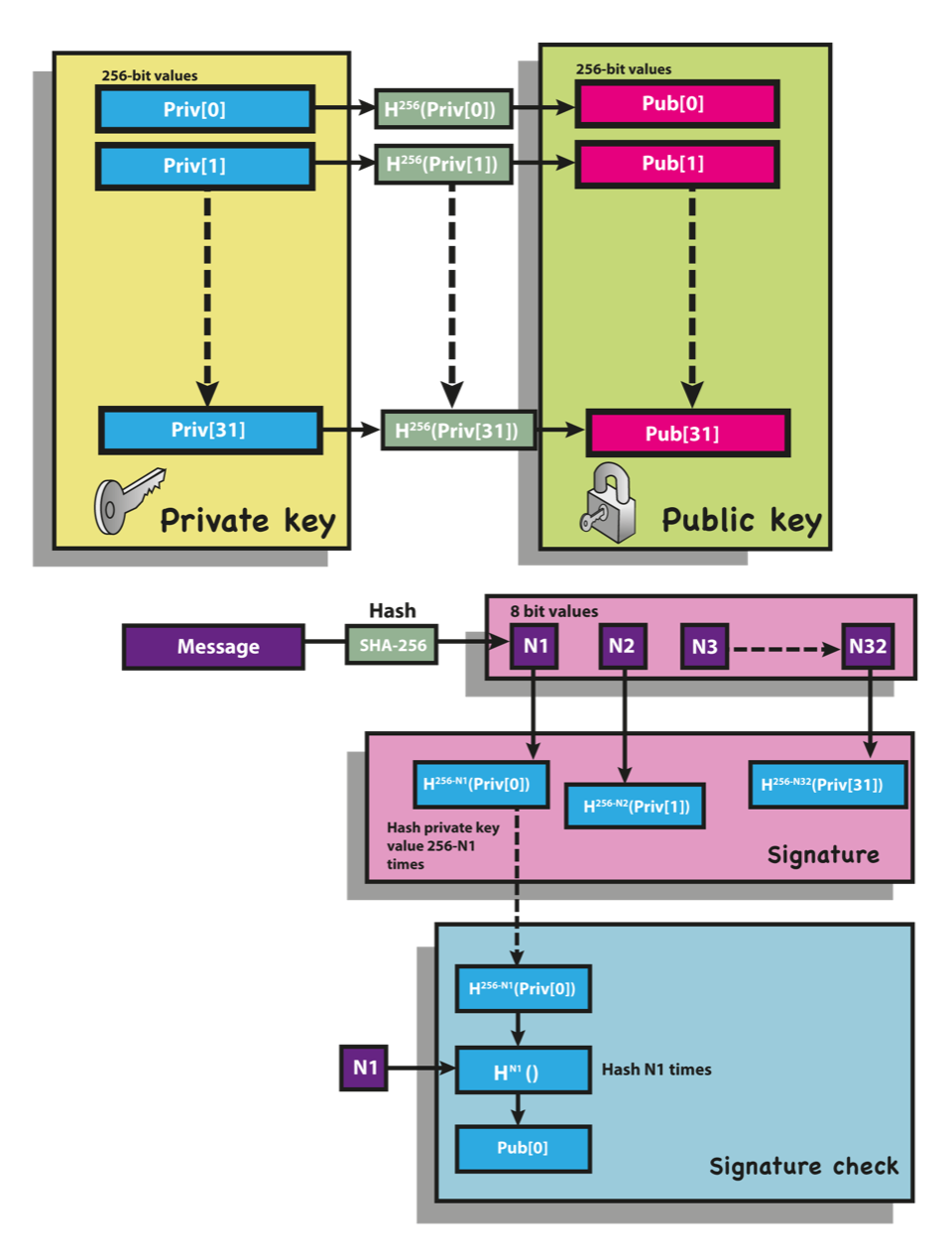
In the Winternitz OTS scheme, the private key is generated differently. The private key consists of an array of integers rather than a matrix of binary digits. Each integer in the array corresponds to a number of times a one-way function is iteratively applied to a randomly generated seed. The resulting output of the function is used to derive a public key.

To sign a message using Winternitz OTS, the signer first hashes the message using a one-way function. The hash output is then split into a fixed number of equal-sized pieces, and each piece is mapped to an index in the private key array. The value stored at the indexed position in the array is then subtracted from a fixed constant (usually the maximum possible value that an integer can represent). The resulting value is then iteratively hashed using the one-way function a number of times corresponding to the value that was subtracted. The final output of the function is the signature.

To verify the signature, the receiver uses the public key to regenerate the same sequence of hashes as the signer. The resulting hash output is compared to the signature to determine its validity.

The main advantage of the Winternitz OTS scheme over the Lamport OTS scheme is that it requires fewer bits in the private key, resulting in smaller keys and signatures. This makes it more efficient and practical for use in resource-constrained environments. However, it is also more vulnerable to attack since an attacker can forge signatures by guessing the value at a specific position in the private key array.

Technical Details

The W-OTS scheme follows the Lamport signature approach but allows a signer to sign w bits of a message-digest simultaneously rather than 1. This collection of bits is a treated as a "digit" of base 2^w.

For example, in the case of w=8 the digits simply become bytes since each digit can take any value within 0..255. The fundamental cryptographic mechanism in W-OTS is the ability to sign individual digits using a unique "digit private key".

For example, to sign the byte b (for w=8), a signer first derives a "private digit key" as K = H(secret) and a "public digit key" P = H^255(K). Notice that all the values of b map to a unique hash in that chain of hashes. The signer advertises the "public digit key" prior to signing any digit. When signing a digit b, the signer provides the verifier the value S=H^(255-b)(K) referred to as the "signature of b". The verifier need only perform b more iterations on the signature s to arrive at the public key P, since H^b(S) = H^b(H^(255-b)(K)) = H^255(K) = P.

At this point, the verifier has cryptographically determined the signer had knowledge of K since the signature S was the b'th pre-image of P. This process of signing digits is repeated for each digit in the message and each digit signature is concatenated to form the signature. The message being signed is always a digest of an actual logical message, and thus referred to as the "message-digest".

In W-OTS, the individual "digit keys" and "digit signatures" are concatenated to comprise the "key" and "signatures" respectively. This results in order of magnitude larger key and signature objects when compared to traditional elliptic-curve / discrete logarithm schemes. This is a significant down-side of OTS schemes when used in post-quantum cryptography (PQC) use cases. The burden of large keys can be optimized by using the hash of a public key as WAMSD prescribes. The burden of large signatures can be halved by choosing shorter hash functions without impacting security, as prescribed by the W-OTS#4 variant. .