RandomHash

  PIP: PIP-0009
  Title: RandomHash: GPU & ASIC Resistant Hash Algorithm
  Type: Protocol
  Impact: Hard-Fork
  Author: Herman Schoenfeld
  Comments-URI: https://discord.gg/sJqcgtD  (channel #pip-0009)
  Status: Active
  Created: 2017-12-17
  Updated: 2017-12-29 (rev2), 2018-01-01 (typos), 2018-02-06 (rev3), 2018-08-17 (rev4)



						

Summary

A GPU and ASIC resistant hashing algorithm change is proposed in order to resolve the current mining centralization situation and to prevent future dual-mining centralization.

Motivation

PascalCoin is currently experiencing 99% mining centralization by a single pool which has severely impacted ecosystem growth and adoption. Exchanges are reticent to list PASC due to the risk of double-spend attacks and infrastructure providers are reticent to invest further due to low-volume and stunted price-growth.

Background

PascalCoin is a 100% original Proof-of-Work coin offering a unique value proposition focused on scalability. After the initial launch, a healthy decentralized mining community emerged and became active in the coins ecosystem, as expected. However, after 9 months a single pool (herein referred to as Pool-X) managed to centralize mining over a short period of time. At the time, it was believed that a technical exploit was being employed by Pool-X, but this possibility was ruled out after exhaustive analysis and review by the developers and 3rd parties. It is now understood why and how this centralization occurred, and how it can be fixed.

It’s an economics issue, not a technical issue. Since PascalCoin is GPU-friendly PoW coin, it has become a prime candidate for "dual-miners", especially Ethereum-centric Pool-X. Dual-miners are miners who mine two independent coins simultaneously using the same electricity. This works because some coins are memory-hard (Ethereum) and others are not (PascalCoin). When mining memory-hard coins, GPUs have an abundance of idle computational power which can be re-purposed to simultaneously mine a non-memory-hard coin like PascalCoin. Whilst a great technical innovation, the introduction of dual-mining has fundamentally changed the economics and incentive-model of mining for the "secondary coin".

Ordinarily, a coins mining ecosystem grows organically with interest and centralization does not occur. This is due to the "hash-power follows price" law. As price grows organically due to interest, so do the number of miners. If there are too many miners, the coin becomes unprofitable, and some miners leave. This homeostasis between mining, price and ecosystem size is part of the economic formula that makes cryptocurrencies work.

With dual-mining, this is broken. Dual-mining has led to coins with small user-base having totally disproportionate number of miners who mine the coin even when "unprofitable". In the case of PascalCoin, miners are primarily on Pool-X to mine Ethereum, not PascalCoin. So the number of PascalCoin miners are a reflection of Ethereum's ecosystem, not PascalCoin's. Also, these miners mine PascalCoin because they have latent computing power, so it technically costs them nothing to mine PascalCoin. As a result, they mine PascalCoin even when unprofitable thus forcing out ordinary miners who are not dual-mining.

These mis-aligned economic incentives result in a rapid convergence to 99% centralization, even though no actor is malicious.

Specification

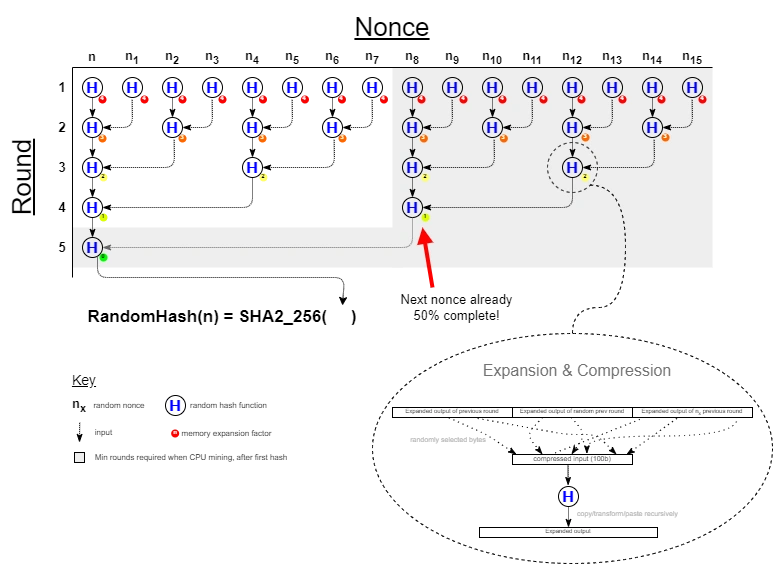
A low-memory, GPU and ASIC-resistant hash algorithm calledRandom Hash is proposed to resolve and prevent dual-mining centralization. Random Hash, defined first here, is a "high-level cryptographic hash" algorithm that combines other well-known hash primitives in a highly serial manner. The distinguishing feature is that calculations for a nonce are dependent on partial calculations of other nonces, selected at random. This allows a serial hasher (CPU) to re-use these partial calculations in subsequent mining saving 50% or more of the work-load. Parallel hashers (GPU) cannot benefit from this optimization since the optimal nonce-set cannot be pre-calculated as it is determined on-the-fly. As a result, parallel hashers (GPU) are required to perform the full workload for every nonce. Also, the algorithm results in 10x memory bloat for a parallel implementation. In addition to it's serial nature, it is branch-heavy and recursive making in optimal for CPU-only mining.

Overview

1. Hashing a nonce requires N iterations (called rounds)
2. Each round selects a random hash function from a set of 18 well-known hash algorithms
3. The input at round x is salted with the outputs of all prior rounds
4. The input at round x is salted with the output of all prior roundsof a different nonce, randomly determined
5. The input at round x is a compression of the transitive closure of prior/neighbouring round outputs to the size of 100 bytes
6. The output of every round is expanded for memory-hardness
7. Randomness is generated using Mersenne Twister algorithm
8. Randomness is seeded via MurMur3 checksum of current round
9. The final round is then hashed again via SHA2_256, in keeping with traditional cryptocurrency approaches.

RandomHash Design

    const
        HASH_ALGO = [
            SHA2_256
            SHA2_384
            SHA2_512
            SHA3_256,
            SHA3_384,
            SHA3_512,
            RIPEMD160,
            RIPEMD256,
            RIPEMD320,
            Blake2b, 
            Blake2s,
            Tiger2_5_192,
            Snefru_8_256,
            Grindahl512,
            Haval_5_256,
            MD5
            RadioGatun32
            Whirlpool
        ]
        N = 5           // Number of hashing rounds required to compute a nonce (total rounds = 2^N - 1)
        M = 10KB        // The memory expansion unit (in bytes)

        Function RandomHash(blockHeader : ByteArray) : ByteArray
        begin
            let allOutputs = RandomHash( blockHeader, N)
            Result := SHA2_256( Compress( allOutputs ) )
        end

        Function RandomHash(blockHeader : ByteArray, Round : Integer) : List of ByteArray
        begin
            if Round < 1 or Round > N then
                Error 'Round must be between 0 and N inclusive'

            let roundOutputs = new List of ByteArray
            
            if Round = 1 then
                let seed = Checksum(blockHeader)      // can hash blockHeader first, but not required
                let gen = RandomNumberGenerator(seed)
                let roundInput = blockHeader
            else
                let parentOutputs = RandomHash(blockHeader, Round - 1)
                let seed = Checksum(parentOutputs)
                let gen = RandomNumberGenerator(seed)

                roundOutputs.AddMany(parentOutputs)
                
                let otherNonceHeader = ChangeNonce(blockHeader, gen.NextDWord)
                let neighborOutputs = RandomHash(otherNonceHeader, Round - 1)
                roundOutputs.AddMany(neighborOutputs)
                
                let roundInput = Compress(roundOutputs)
            
            let hashFunc = HASH_ALGO[gen.NextDWord % 18]   
            let output = hashFunc(roundInput)                
            output = Expand( output, N - Round )
            roundOutputs.Add(output)

            Result := roundOutputs
        end


        Function Expand(input : ByteArray, ExpansionFactor : Integer) : ByteArray
        begin
            let seed = Checksum(input)
            let gen = RandomNumberGenerator(seed)
            let size = Length(input) + ExpansionFactor*M
            let output = input.Clone
            let bytesToAdd = size - Length(input)
            while bytesToAdd > 0 do
                let nextChunk = output.Clone
                if Length(nextChunk) > bytesToAdd then
                    SetLength(nextChunk, bytesToAdd)

                let random = gen.NextDWord
                case random % 8 do
                    0: output = output ++ MemTransform1(nextChunk)
                    1: output = output ++ MemTransform2(nextChunk)
                                .
                                .
                                .
                    7: output = output ++ MemTransform8(nextChunk)
                bytesToAdd = bytesToAdd - Length(nextChunk)
            Result = output
        end

        Function Compress(inputs : list of ByteArray) : ByteArray
        begin
            let seed = Checksum(inputs)
            let gen = RandomNumberGenerator(seed)
            let output = Byte[0..99]
            for i = 0 to 99 do
                let source = inputs[ gen.NextDWord % Length(inputs) ]
                output[i] = source[ gen.NextDWord % Length(source) ]
            Result := output
        end 

        Function ChangeNonce(blockHeader : ByteArray, nonce : Integer) : ByteArray
        begin
            // clones and changes nonce in blockHeader (by determining offset of nonce)
        end

        Function Checksum(input : ByteArray) : DWord
        begin
            // standard MurMu3 algorithm
        end
    
        Function Checksum(inputs : List of ByteArray) : DWord
        begin
            // standard MurMu3 algorithm run over list of inputs
        end

        Function RandomNumberGenerator(seed : DWord) : TMersenneTwister
            // standard Mersenne Twister random number generator (or other suitably chosen algorithm)
        end


						

RandomHash pseudo-code

Memory transform methods

These methods are iteratively and randomly applied to a hash output in order to rapidly expand it for compression in the next round.Note: the length of the output is always the same as the length of the input.

     - Memory Transform 1: XorShift32    (e.g. input = 1234567  output = select random from input using XorShift32 RNG
     - Memory Transform 2: Swap-LR       (e.g. input = 1234567  output = 5674123)   
     - Memory Transform 3: Reverse       (e.g. input = 1234567  output = 7654321)  
     - Memory Transform 4: L-Interleave  (e.g. input = 1234567  output = 1526354)
     - Memory Transform 5: R-Interleave  (e.g. input = 1234567  output = 5162734)
     - Memory Transform 6: L-XOR         (e.g. input = 1234567  output = XOR(1,2), XOR(3,4), XOR(5,6), 7, XOR(1,7), XOR(2,6), XOR(3,5)
     - Memory Transform 7: ROL-ladder    (e.g. input = ABCDEF   output = ROL(A, LENGTH - 0), ROL(B, LENGTH - 1), ... , ROL(F, LENGTH - 5)
     - Memory Transform 8: ROR-ladder    (e.g. input = ABCDEF   output = ROR(A, LENGTH - 0), ROR(B, LENGTH - 1), ... , ROR(F, LENGTH - 5)


						

Formal definitions are as follows:

Memory Transform 1

This selects random bytes for AChunk using XorShift32 RNG. The initial seed is the CHECKSUM of AChunk. If CHECKSUM is 0 then 1 is used instead.

    function MemTransform1(AChunk: TBytes): TBytes
    var
      i, LChunkLength : UInt32
      LState : UInt32

      function XorShift32 : UInt32 inline
      begin
        LState := LState XOR (LState SHL 13)
        LState := LState XOR (LState SHR 17)
        LState := LState XOR (LState SHL 5)
        Result := LState
      end

    begin
      // Seed XorShift32 with non-zero seed (checksum of input or 1)
      LState := Checksum(AChunk)
      if LState = 0 then
        LState := 1

      // Select random bytes from input using XorShift32 RNG
      LChunkLength := Length(AChunk)
      SetLength(Result, LChunkLength)
      for i := 0 to High(AChunk) do
        Result[i] := AChunk[XorShift32 MOD LChunkLength]
    end


						

Memory Transform 2

    function MemTransform2(AChunk: TBytes): TBytes
    var
      i, LChunkLength, LPivot, LOdd: Int32
    begin
      LChunkLength := Length(AChunk)
      LPivot := LChunkLength SHR 1
      LOdd := LChunkLength MOD 2
      SetLength(Result, LChunkLength)
      Move(AChunk[LPivot + LOdd], Result[0], LPivot)
      Move(AChunk[0], Result[LPivot + LOdd], LPivot)
      // Set middle-byte for odd-length arrays
      if LOdd = 1 then
        Result[LPivot] := AChunk[LPivot]
    end


						

Memory Transform 3

    function MemTransform3(AChunk: TBytes): TBytes
    var
      i, LChunkLength: Int32
    begin
      LChunkLength := Length(AChunk)
      SetLength(Result, LChunkLength)
      for i := 0 to High(AChunk) do
        Result[i] := AChunk[LChunkLength - i - 1]
    end


						

Memory Transform 4

    function MemTransform4(AChunk: TBytes): TBytes
    var
      i, LChunkLength, LPivot, LOdd: Int32
    begin
      LChunkLength := Length(AChunk)
      LPivot := LChunkLength SHR 1
      LOdd := LChunkLength MOD 2
      SetLength(Result, LChunkLength)
      for i := 0 to LPivot - 1 do
      begin
        Result[(i * 2)] := AChunk[i]
        Result[(i * 2) + 1] := AChunk[i + LPivot + LOdd]
      end
      // Set final byte for odd-lengths
      if LOdd = 1 THEN
        Result[High(Result)] := AChunk[LPivot]
    end


						

Memory Transform 5

    function MemTransform5(AChunk: TBytes): TBytes
    var
      i, LChunkLength, LPivot, LOdd: Int32
    begin
      LChunkLength := Length(AChunk)
      LPivot := LChunkLength SHR 1
      LOdd := LChunkLength MOD 2
      SetLength(Result, LChunkLength)
      for i := 0 to LPivot - 1 do
      begin
        Result[(i * 2)] := AChunk[i + LPivot + LOdd]
        Result[(i * 2) + 1] := AChunk[i]
      end
      // Set final byte for odd-lengths
      if LOdd = 1 THEN
        Result[High(Result)] := AChunk[LPivot]
    end


						

Memory Transform 6

    function MemTransform6(const AChunk: TBytes): TBytes
    var
      i, LChunkLength, LPivot, LOdd: Int32
    begin
      LChunkLength := Length(AChunk)
      LPivot := LChunkLength SHR 1
      LOdd := LChunkLength MOD 2
      SetLength(Result, LChunkLength)
      for i := 0 to Pred(LPivot) do
      begin
        Result[i] := AChunk[(i * 2)] xor AChunk[(i * 2) + 1]
        Result[i + LPivot + LOdd] := AChunk[i] xor AChunk[LChunkLength - i - 1]
      end
      // Set middle-byte for odd-lengths
      if LOdd = 1 THEN
        Result[LPivot] := AChunk[High(AChunk)]
    end


						

Memory Transform 7

    function MemTransform7(AChunk: TBytes): TBytes
    var
      i, LChunkLength: Int32
    begin
      LChunkLength := Length(AChunk)
      SetLength(Result, LChunkLength)
      for i := 0 to High(AChunk) do
        Result[i] := TBits.RotateLeft8(AChunk[i], LChunkLength - i)
    end


						

Memory Transform 8

    function MemTransform8(AChunk: TBytes): TBytes
    var
      i, LChunkLength: Int32
    begin
      LChunkLength := Length(AChunk)
      SetLength(Result, LChunkLength)
      for i := 0 to High(AChunk) do
        Result[i] := TBits.RotateRight8(AChunk[i], LChunkLength - i)
    end


						

RandomHash Analysis

CPU Bias

The RandomHash algorithm is inherently biased towards CPU mining due to it's highly serial nature. In addition, RandomHash allows CPU miners to cache the partial calculations of the other nonces and resume them later. This allows CPU miners to save 50% of the work during mining. This is formally proven below, but is easy to grasp as follows - in order to complete a nonce to round N, another nonce needed to be completed to round N-1. The other nonce requires 1 more round to complete, saving 50% of the work. This optimal nonce-set cannot be pre-calculated, and can only be enumerated. As a result, serial mining (CPU) does 50% the work of parallel mining (GPU).

Memory Complexity

RandomHash is memory-light in order to support low-end hardware. A CPU will only need 5MB of memory to verify a hash. During mining, it will need 10MB per thread (when utilizing the 50% bias mentioned above) -- an easy requirement. It's important to note that RandomHash consumes most of the memory in the initial rounds and little in the final rounds. This is deliberate in order to hinder GPU mining. For example, suppose a GPU has 5GB of memory. A naive hasher could attempt to batch 1000 nonces for parallel evaluation (since each nonce requires 5MB). However, since each nonce depends on 15 other nonces and most of the "5MB per nonce" is consumed in the early rounds of those nonce evaluations, the GPU will run out of memory quickly. The batch size needs to be divided by 15 in order to utilize the 5GB effectively, which means most of the GPU memory is wasted on partial nonce calculations from the early rounds. In that scenario, the GPU can only effectively compute 20 nonces per 1GB of memory. A CPU can easily compete with this and implement intelligent parallel mining by using other threads to mine the less-partially calculated nonces. This could potentially give a CPU significantly greater than 50% advantange, but this approach needs further research.

GPU Resistance

GPU performance is generally driven by parallel execution of identical non-branching code-blocks across private regions of memory. Due to the inter-dependence between hashing rounds, the slower global memory will need to be used. Also, due to the highly serial nature of RandomHash's algorithm, GPU implementations will be inherently inefficient. In addition, the use of Mersenne Twister to generate random numbers and the use of recursion will result in executive decision making further degrading GPU performance. Most importantly, since nonce's are inter-dependent on other random nonces, attempts to buffer many nonces for batch hashing will result in high memory-wastage and 200% more work than a CPU. This occurs because each buffered nonce will require calculation of many other unbuffered dependent nonces, rapidly consuming the available memory. A CPU implementation does not suffer this since the optimal nonce-set to mine is enumerated on-the-fly as each nonce completes. Another important feature is the pattern of memory expansion factors chosen for each round. These were deliberately chosen to hinder GPUs by amplifying the memory needed for their wasted calculations.

As a result, it's expected that GPU performance will at best never exceed CPU performance or at worst perform only linearly better (not exponentially as is the case now with SHA2-256D).

ASIC Resistance

ASIC-resistance is fundamentally achieved on an economic basis. Due to the use of 18 sub-hash algorithms, it is expected that the R&D costs of a RandomHash ASIC will mirror that of building 18 independent ASICs. This moves the economic viability goal-posts away by an order of magnitude. For as long as the costs of general ASIC development remain in relative parity to the costs of consumer grade CPUs as of today, a RandomHash ASIC will always remain "not worth it" for a "rational economic actor".

Furthermore, RandomHash offers a wide ASIC-breaking attack surface. This is due to it's branch-heavy,serial, recursive nature and heavy dependence on sub-algorithms. By making minor tweaks to the high-level algorithm, or changing a sub-algorithm, an ASIC design can be mostly invalidated and sent back the drawing board.

This is true since ASIC designs tend to mirror the assembly structure of an algorithm rather than the high-level algorithm itself. Thus by making relatively minor tweaks at the high-level that necessarily result in significant low-level assembly restructuring, an ASIC design is made obsolete. So long as this "tweak-to-break-ASIC" policy is maintained by the PascalCoin Developers and Community, ASIC resistance is guaranteed.

RandomHash Variations

Variations of RandomHash can be made by varying N (the number of rounds required) and M (the memory expansion). For non-blockchain applications, the dependence on other nonces can be removed, providing a cryptographically secure general-purpose, albeit slow, secure hasher.

It is also possible to change the dependence graph between nonces for stronger CPU bias. For example, requiring the lower rounds to depend on more than one nonce and the upper rounds on no nonces at all, may allow further CPU vs GPU optimization. Similarly, for memory expansion factors.

Extra, albeit unnecessary, strengethening can be added in the initial rounds of hashing by using the hash of the blockheader for seeding, instead of the blockheader itself. In the analysis of the author, this is unnecessary and has subsequently been removed.

Formal Proofs

This section proves some of the claims made in this PIP.

Let N = the number of rounds required to complete a single RandomHash

Let M = the memory unit to expand out a hash's output by

Hash Complexity

Let F(x) denote number of hashes required at round x.

Since the first round just hashes the block header, the base case for F is

F(1) = 1

Since a hash at round x is the hash of the previous roundand of round x-1 of another nonce

    F(x) = 1 + F(x-1) + F(x-1)


						

NOTE: complexity associated with expansion and contraction is ommitted here, since only interested in Hash complexity.

Simplifying

    F(x) = 1 + 2 F(x-1) 
         = 1 + 2(1 + 2 F(x-2)) 
         = 1 + 2^1 + 2^2 + 2^3 + ... + 2^(x-1)
         = SUM(i=0, x-1) 2^i
         = 2^x - 1


						

Adding the final "veneer" SHA2-256 round of RandomHash to 2^x - 1 gives:

    F(x) = 2^x


						

Memory Consumption

Let G(N) denote the minimum amount of memory required for a RandomHash of a single nonce. Here N denotes the number of rounds required in RandomHash.

Firstly, after a full RandomHash involving N rounds, the total count of hashes at any round x is

    TotalHashesAtRound(x) = 2^(N-x)


						

It follows that the total memory for the round is calculated as follows

    TotalMemoryAtRound(x) = (N-x) * TotalHashesAtRound(x)
                          = 2^(N-x) * (N-x)


						

This can be seen by observing the memory-expansion factors in the diagram. Notice it starts at N-1 for the first round and decreases every subsequent round.

The total memory consumed (in units M) is denoted G(N), and is simply the sum of all the memory at each round

    G(N) = M * sum(i=1, N) TotalMemoryAtRound(i)
         = M * sum(i=1, N) 2^(N-i) * (N-i)
         = M * (2^N (N-2) + 2)


						

Thus,

    G(N) = M * (2^N (N-2) + 2)


						

NOTE: For PascalCoin, N=5 which results 98 units of memory for every single nonce. Choosing memory unit M=50kb results in approximately 4.8MB per nonce. Quite low for a CPU, but bloats quickly for a GPU as mentioned below.

CPU Bias

To show that CPU does 50% the hashing work of a GPU consider that

• N rounds are required to complete a single nonce
• After the completion of any nonce, another nonce is known and pre-computed to round N-1
• For serial mining (CPU), almost all nonce hashing are simply the resumption of a previous pre-computed nonce to N-1. Thus it only does F(N-1) the work.
• For parallel mining (GPU), all the work F(N) must be performed for every nonce.

Thus the work a CPU does is

CPU Work = F(N-1) 
         = 2^(n-1) - 1


						

However GPU does the entire work for every nonce

GPU Work = F(N)
         = 2^n - 1


						

The efficiency is

Efficiency = (CPU Work) / (GPU Work)
           = (2^(N-1)-1) / (2^N - 1)


						

Taking the limit as N approaches +inf = 0.5

Thus a CPU does 50% the work of a GPU.

Hard-Fork Activation

The PIP requires a hard-fork activation involving various aspects discussed below.

Consensus

Since this is a significant change, the PascalCoin community will be asked to vote on this proposal by changing their account types to numbers which correspond to YES or NO votes respectively. All other numbers will be considered ABSTAIN. The total PASC and PASA will be tallied.

Example:
    Account 9876-54 with 0 PASC is considered 1 votes
    Account 1234-56 with 100 PASC is considered 101 votes


						

Implementation

If after a period of time and consensus is reached, RandomHash will be merged into the PascalCoin code-base by the PascalCoin developers. After thorough testing on TestNet, a suitable activation date will be chosen to allow the ecosystem to adopt this mandatory upgrade. A release will be made and notifications provided of activation within the time-frame.

Difficulty Reset

On activation, the block difficulty will be reset to an appropriately low number. During this period, the block times will be highly unstable but will stabilize over approximately 200 blocks. Exchanges are recommended to pause deposits and withdrawals 1 hour before activation and 10 hours after.

Rationale

Aside from a hash algorithm change, the only other known option to resolve 99% mining centralization is to encourage other large Ethereum mining pools to duplicate Pool-X's features thus incentivizing decentralized ETH-PASC dual-mining. Even if this were achieved, it would still price-out ordinary PASC-pools and solo-miners, which is undesirable. It would also fundamentally link the two ecosystems together for no good reason. Efforts to encourage other dual-miners were undertaken but have failed. As a result, this option is no longer considered viable. Changing the hash algorithm is now the only known option to resolve this centralization.

Within the scope of changing the hash algorithm, other hash algorithms were considered like Equihash. However, these were ruled out due to their excessive memory consumption contradicting PascalCoin's vision of globally decentralized network that runs fine on low-end hardware available anywhere on this world. Requiring voluminous amounts of fast memory to validate blocks is not consistent with this vision.

Backwards Compatibility

This PIP is not backwards compatible and requires a hard-fork activation. Previous hashing algorithm must be retained in order to validate blocks mined prior to the hard-fork.

Reference Implementation

A reference implementation of RandomHash can be found here .

Acknowledgements

Refinements to improve GPU-hardness were provided by Ian Muldoon. Improvements to memory tansform randomness provided by Polyminer.

Links

1. Mersennne Twister Implementation (Lazarus/FPC)
2. MurMur3 Implementation (Lazarus/FPC)
3. RandomHash Reference Implementation